17:25 Математик нашел новый способ быстро умножать простые числа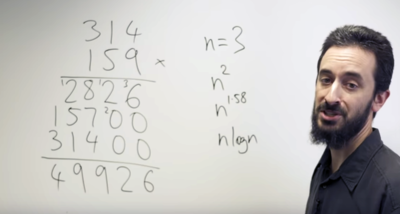 |
|
Умножение длинных чисел в уме — настоящая головная боль для всех детей с самой начальной школы. Однако математик разработал новый метод умножения больших чисел, который намного эффективнее привычного нам. Дэвид Харли, доцент из Университета Нового Южного Уэльса в Сиднее обратился к алгоритму Шёнхаге — Штрассена, разработанному двумя немецкими математиками. В период с 1971 года по 2007 это был самый быстрый способ умножения чисел, пока ему на смену не пришла альтернатива (справедливости ради стоит отметить, что используют ее крайне редко). Шенхаге и Штрассен предсказали существование алгоритма умножения n-значных чисел с использованием базовых операций формата n * log (n). С тех пор прошло несколько десятилетий, но лишь теперь появилось первое доказательство этой гипотезы. Так в чем же суть? Для примера Харви выбрал умножение чисел 314 и 159 — с подобными числами мы сталкиваемся каждый день. Обычно, чтобы решить подобное уравнение, большинство людей перемножает каждый отдельный номер, а затем складывают суммы. Так, 9 умножается на 4,1 и 3, затем 5 умножается на 4, 1 и 3, и так далее. В результате сложения всех результатов и получается искомое 9-значное число. Этот метод называется n2, потому что число n умножается на n несколько раз. Получите ли вы правильный ответ? Безусловно. Однако еще в 1971 году немцы придумали, как ускорить процесс. Они записывали его как n * log (n). Напомним, что log — это сокращение от «логарифма», который помогает нам расшифровывать числа, возведенные в степень. Например, 2⁵ = 32, но если записать это уравнение логарифмически, то получится log₂ (32) = 5. Звучит просто, однако по‑настоящему логарифмы начинают упрощать процесс в работе с крупными числами. Харви уверен, что метод Шёнхаге-Штрассена очень практичен. По его словам, если обычному компьютеру дать задачу перемножить между собой два числа с миллиардом знаков в каждом, используя «школьный» метод — это заняло бы месяцы. А если дать ему ту же задачу, но использовать при этом подход с логарифмами, то вся операция займет… от силы секунд 30. Впрочем, и тут есть пределы. математик отмечает, что если число знаков будет составлять триллион и больше, то здесь пригодится алгоритм, разработанный Харви и его сотрудником Йорисом ван дер Хувеном в Политехнической школе во Франции в 2007 году. «С его помощью можно будет вычислить значение числа «пи» с еще большей точностью. Человечество 50 лет охотилось за таким удобным способом работы с огромными простыми числами — и теперь он наконец в нашем распоряжении», говорит сам Харви. |
|
|
| Всего комментариев: 0 | |
По этой теме смотрите:

ВСЕ НОВОСТИ:
| Астрология, пророчества [1066] | Астрономия и космос [1457] | Безумный мир [2063] |
| Войны и конфликты [2310] | Гипотезы и версии [3874] | Дом,сад,кулинария [3945] |
| Животные и растения [2669] | Здоровье,психология [4748] | История и археология [4652] |
| Мир вокруг нас [2167] | Мировые новости [7583] | Наука и технологии [890] |
| Непознанное [4196] | НЛО,уфология [1263] | Общество [7795] |
| Прогнозы ученых,исследования [798] | Происшествия,чп,аварии [1302] | Российские новости [5860] |
| Стихия,экология,климат [2739] | Феномены и аномалии [945] | Фильмы и видео [6336] |
| Частное мнение [4911] | Это интересно! [3311] | Юмор,афоризмы,притчи [2394] |
АРХИВ САЙТА:
| Астрология и пророчества [825] | Гипотезы и прогнозы [4629] | Дом,сад,кулинария [223] |
| Животные и растения [2796] | Здоровье и красота [5708] | Интересности и юмор [3758] |
| История и археология [4696] | Космос, астрономия [2263] | Мир вокруг нас [1982] |
| Наука и технологии [2422] | Непознанное [3983] | НЛО,уфология [1747] |
| Общество, в мире, новости [11574] | Психология и отношения [84] | Стихия, климат, экология [421] |
| Фильмы и видео [367] | Частное мнения [111] | Эзотерика и феномены [2031] |




