элементарно. Желтый передвигаем под синий, зеленый под желтый, красный вперед

это не пустое место ,а пространство
сказал физик

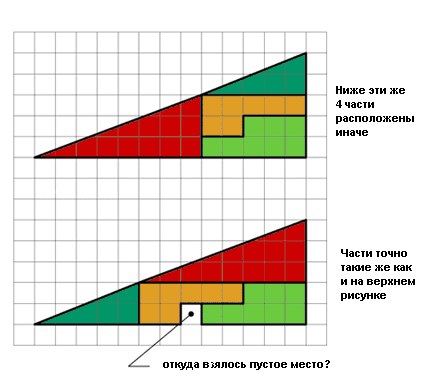
Чуть мозг не вывихнула. Решение лежит в другой плоскости. Это построение на сетке - ловкая иллюзия. Если посчитаете площади двух больших треугольников по обе стороны диагонали, то они должны составлять ровно по половине от площади прямоугольника со сторонами 13 и 5, то есть 65 пополам - 32,5. если же вы будете считать площадь большого треугольника по формуле площадей фигур,то получите: 8*3/2+5*2/2+3*5=12+5+15=32. Получается нестыковка: сумма площадей не равна площади суммы. Этого быть не может.
Далее, верхний треугольник должен быть обратным отражением нижнего, если вы надумаете разделить его на такие же фигуры, а этого не происходит - верхний левый угол, в который должны поместиться зеленая и желтая фигура, составляет 16 клеток, а не 15, как внизу.
Так что, мы имеем дело с оптическим обманом: при разделении прямоугольника диагональю размеры клеток искусственно подогнаны на малую величину - чтобы точка соприкосновения красного и синего треугольников пришлась как раз на узел сетки, а этого как раз и не должно быть. Вот откуда и берется эта дырка - она и составляет разницу в площади верхнего незакрашенного треугольника и нижнего, разделенного на секции.

Обман состоит в том,что мы привыкли мыслить стереотипно, например,исходим из уверенности, что клеточная сетка обязательно соответствует прямоугольной системе координат с равномерным делением - как в школьной тетради, которой мы привыкли доверять. А тут по вертикали имеются чуть заметные сдвиги, что и обеспечивает эту хитрую подгонку.

Очень просто. Гипотенуза не прямая: в первом случае она чуть-чуть выгибается вниз, во втором случае немного вверх. Наклон гипотенузы красного треугольника равен 3/8, а наклон гипотенузы темно-зеленого треугольника равен 2/5. Приводя к одному знаменателю, получаем 15/40 для красного и 16/40 для темно-зеленого. Значит, красная гипотенуза идет более полого. И потому на втором рисунке она отхватывает сверху большее пространство. А т.к. общая площадь неизменна, где-то должен появиться вырез. Вот он и появляется.

Сетка хитро нарисована. В первом треугольнике гипотенуза слегка вогнута, а во втором слегка выпуклая. Впадина и выпуклость приходятся как раз на узел который лежит на гипотенузе. Это отклонение очень маленькое, почти незаметное (приложите линейку). Поэтому верхний треугольник на 0,5 клетки меньше расчетного, а второй на 0,5 больше. Два раза по 0,5 вот и "набежала" 1 пустая клетка

Кстати, если не верите в подгонку, то можете проверить при помощи тангенциальных соотношений для одного и того же угла - левого. Отношение 5 к 13 для большого треугольника - 0,3846. Для красного: 3 к 8 - 0,375. Для синего: 2 к 5 - 0,4 . Они все разные - для одного-то угла! Расхождения незначительны,но они-то и обеспечены погрешностью делений - в данном случае это значимо. Погрешности могут нивелироваться в сумме, а могут и усиливать друг друга,давая в итоге значительную нестыковку - вот как раз этот квадратик.

)) От перестановки слагаемых в сумме появилась брешь. ))

черные линии окантовки имеют толщину и суммарную длину.После перетасовки фигур суммарная длина и ширина черной линии уменьшилась,высвободив площадь примерно в квадрат

Вот ещё http://www.youtube.com/watch?v=hdkf2CsSI7o

Дополнение к №5. Вогнутость и выпуклость просматриваются. Их хорошо скрадывает толщина линии.